1.基本概念

二叉树是树形结构中一种特殊的树形结构：二叉树中的每个结点至多有2棵子树(即每个结点的度小于等于2)，并且两个子树有左右之分，顺序不可颠倒。在二叉树中还有种特殊的二叉树就是完全二叉树：所有结点中除了叶子结点以外的结点都有两棵子树。如果完全二叉树中只有最底层为叶子结点那么又称为满二叉树。

重要性质：

二叉树中，第m-层最多有2^(m-1)个结点(根结点为第一层)

高度为k的二叉树至多有2^k-1个结点

二叉树T叶子结点总数为n0，度为2的结点个数为n2，则n0=n2+1

如果完全二叉树有n个结点，那么树最高为log2(n)+1

对于完全二叉树，从上至下，从左至右对每个结点从1-n编号，那么对于结点n有：

如果i=1，那么此结点为根结点，如果i>1那么该结点的父结点为不大于i/2的最大整数

如果2*i>n，那么i结点没有左子树，如果2*i<=n那么该结点的左子树编号为2*i

如果2*i+1>n，那么结点i没有右子树，如果2*i+1<=n那么该结点的右子树编号为2*i+1

2.抽象数据类型

(1)数据对象集合：二叉树中各个结点的集合。每个结点至多有2个孩子结点，叶子结点没有子结点，每个结点只有一个父结点，根结点没有父结点。

(2)基本操作集合：

InitBitTree(&T):初始化二叉树为一棵空树

CreateBitTree(&T):创建二叉树

DestroyBitTree(&T):删除二叉树

InsertLeftChild(p,c):将二叉树c插入到p所指向的左子树

InsertRightChild(p,c):将二叉树c插入到p所指向的右子树

LeftChild(&T,e):返回左孩子

RightChild(&T,e):返回右孩子

DeleteLeftChild(&T,p):删除左孩子

DeleteRightChild(&T,p):删除右孩子

PreOrderTraverse(T):前序遍历二叉树

InOrderTraverse(T):中序遍历二叉树

PostOrderTraverse(T):后序遍历二叉树

LeverTraverse(T):层次遍历二叉树

BitTreeDepth(T):求二叉树的高度

3.二叉树的存储实现

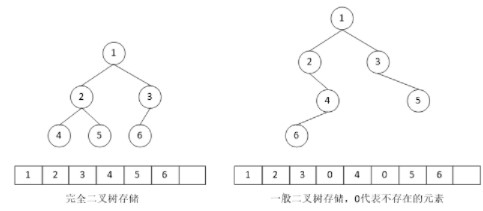
(1)顺序存储：完全二叉树中每个结点的编号可以通过性质求得，所以可以将元素按从上至下、从左至右的顺序放入一维数组中。而对于非完全二叉树，则只需要将相对于完全二叉树缺失的结点用“^"代替。

(2)链式存储：二叉树的链式存储需要三个域存储：数据域、左孩子指针域和右孩子指针域。两个指针域分别指向左右子树。这种存储结构叫做二叉链表存储。如果再加上一个指向父结点的指针域那么就称为三叉链表存储。

动力节点在线课程涵盖零基础入门，高级进阶，在职提升三大主力内容，覆盖Java从入门到就业提升的全体系学习内容。全部Java视频教程免费观看，相关学习资料免费下载!对于火爆技术，每周一定时更新!如果想了解更多相关技术，可以到动力节点在线免费观看数据结构视频教程哦!